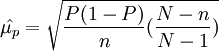什么是抽样误差？抽样误差的计算怎么算？

发布时间: 2023-04-27 10:13:53 来源:百科网

什么是抽样误差？

在抽样检查中，由于用样本指标代替全及指标所产生的误差可分为两种：一种是由于主观因素破坏了随机原则而产生的误差，称为系统性误差;另一种是由于抽样的随机性引起的偶然的代表性误差。抽样误差仅仅是指后一种由于抽样的随机性而带来的偶然的代表性误差，而不是指前一种因不遵循随机性原则而造成的系统性误差。

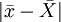
$|\bar{x}-\bar{X}$

总的说来，抽样误差是指样本指标与全及总体指标之间的绝对误差。在进行抽样检查时不可避免会产生抽样误差，因为从总体中随机抽取的样本，其结构不可能和总体完全一致。例如样本平均数与总体平均数之差，样本成数与总体成数之差|p−P|。虽然抽样误差不可避免，但可以运用大数定律的数学公式加以精确地计算，确定它具体的数量界限，并可通过抽样设计加以控制。

抽样误差也是衡量抽样检查准确程度的指标。抽样误差越大，表明抽样总体对全及总体的代表性越小，抽样检查的结果越不可靠。反之，抽样误差越小，说明抽样总体对全及总体的代表性越大，抽样检查的结果越准确可靠。在统计学中把抽样误差分为抽样平均误差和抽样极限误差，下面就这两种误差分别进行阐释。为使推理过程简化，这里不对属性总体进行分析，而仅对变量总体进行分析计算。

抽样误差的计算怎么算？

1、表现形式：平均数指标抽样误差;成数(比重)抽样误差。

2、平均数指标的抽样误差

1)重复抽样的条件下：

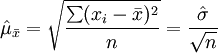
$\hat{\mu}_{\bar{x}}=\sqrt{\frac{\sum(x_i-\bar{x})^2}{n}}=\frac{\hat{\sigma}}{\sqrt{n}}$

2)不重复抽样的条件下：

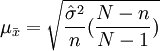
$\mu_{\bar{x}}=\sqrt{\frac{\hat{\sigma}^2}{n}(\frac{N-n}{N-1})}$

3、成数指标的抽样误差

1)重复抽样的条件下：

$\hat{\mu_p}=\sqrt{\frac{P(1-P)}{n}}$

2)不重复抽样的条件下：

$\hat{\mu_p}=\sqrt{\frac{P(1-P)}{n}(\frac{N-n}{N-1})}$

什么是抽样误差？抽样误差的计算怎么算？

相关文章Related